Korelace je pojem, popisující statistickou závislost mezi minimálně dvěma parametry.
Na co slouží korelace
Korelace slouží ke stanovení statistické závislosti závisle proměnné (tu potřebujeme zjistit) od nezávisle proměnné (tu známe nebo ji umíme nastavovat). Korelace se většinou používá pro odhad hodnoty závisle proměnné, to znamená predikci určitého stavu. Je to jednoduchý statistický model systému.
Korelace může být jednoduchá, tehdy stanovuji souvislost mezi jednou nezávisle proměnnou a jednou závisle proměnnou. Je to nejčastější typ korelace.
Komplexnějšími jsou tzv. vícenásobná korelace popisující souvislost jedné závisle proměnné od několika nezávislých proměnných.
Pro korelaci platí omezení vyplývající z její podstaty. Korelace popisuje výlučně statistickou závislost, nikoli kauzální. Mezi nezávislou a závislou proměnnou nemusí být vůbec žádný přímý vztah.
Rozdíl mezi kauzální a statistickou závislostí si můžeme demonstrovat na následujícím příkladu:
V New Yorku zkoumali několik faktorů v souvislosti s kriminalitou a zjistilo se, že existuje silný korelační vztah mezi počtem prodaných zmrzlin a počtem vykradených bytů. Pokud počet prodaných zmrzlin stoupal, stoupal i počet krádeží. Navzdory silné statistické korelace neexistuje kauzální příčina mezi prodejem zmrzliny a počtem krádeží.
Druhým omezením je fakt, že hodnoty závisle proměnné je možné předpovědět pouze v rámci rozsahu nezávisle proměnné, ve kterém se statistická závislost určila. Například, pokud budu měřit teplotu vzduchu v závislosti na denní doby v měsíci červnu, tak mohu odhadnout teploty vzduchu v určité hodině pouze pro měsíc červen. Pro měsíc leden odhad hodnot nemohu použít.
Protože korelace určuje tzv. statistickou závislost, nikoli kauzální (příčina-následek) není ani při silné korelací možné určit hodnotu neznámého parametru se 100% jistotou.
Použití v praxi
Zkoumání korelační závislosti je možné provést po současném naměření dostatečného počtu závislé a nezávislé proměnné. Ve druhém kroku se určuje korelační závislost mezi závislou proměnnou a nezávislou proměnnou, případně proměnnými. Zkoumá se těsnost korelace (síla korelace) a tvar křivky, která reprezentuje závislost. V nejjednodušším případě popisuje vztah mezi závislou proměnnou a jednou nezávislou proměnnou přímka. V tomto případě říkáme o lineární závislosti. Vyjádřením závislosti je rovnice přímky ve tvaru y = ax + b, kde y je závisle proměnná a x je nezávisle proměnná.
Na vyjádření těsnosti korelace se používá korelační koeficient, který nabývá hodnoty od -1 po 1. V praxi se používá jeho druhá mocnina. Pokud je korelační koeficient kladný, mezi proměnnými je přímá úměra. Pokud je záporný, mezi proměnnými je nepřímá úměra. Pokud je koeficient roven nule, obě proměnné jsou statisticky nezávislé.
Grafickým vyjádřením závislosti je korelační graf, kde na ose x jsou vyneseny hodnoty nezávisle proměnné a na y ose závisle proměnné. Naměřenými body je přeložena tzv. regresní křivka, která reprezentuje funkci závislosti proměnných. Její "přesnost" vyjadřuje korelační koeficient, respektive jeho druhá mocnina. Čím více se hodnota druhé mocniny blíží 1, tím přesněji víme určit na základě regresní rovnice hodnotu závisle proměnné z hodnoty nezávisle proměnné. Pokud je korelační koeficient roven 0 (jeho druhá mocnina je pak také rovna 0), z hodnoty nezávisle proměnné neumíme určit hodnotu závisle proměnné. Závisle proměnná se chová jako náhodná veličina, jejíž hodnotu neovlivňuje hodnota nezávisle proměnné.
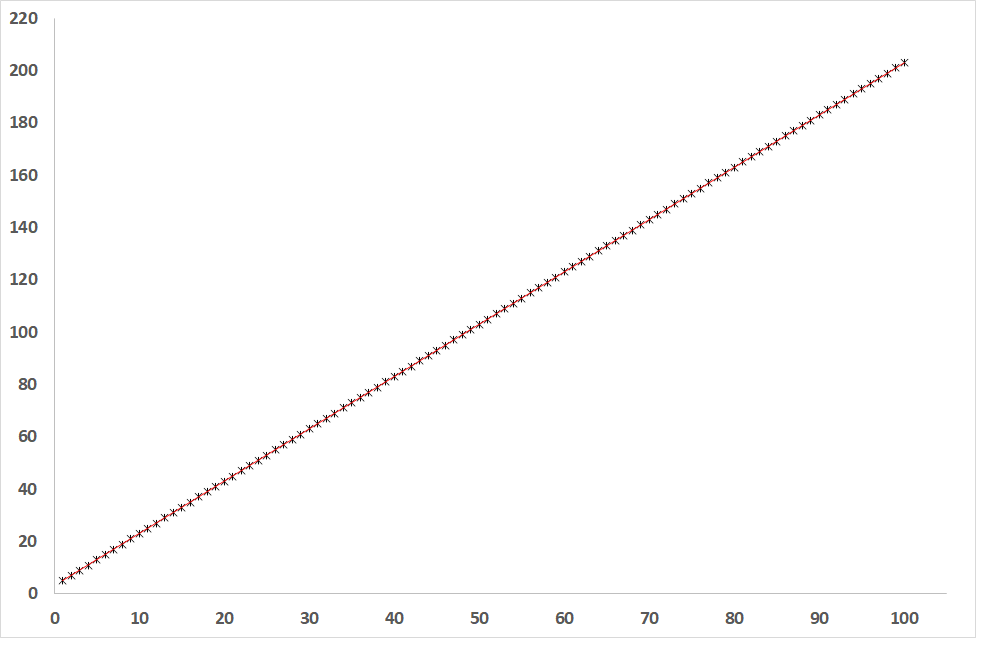 Obr. 1: Závislost závisle proměnné od nezávisle proměnné, pokud je R = 1 (přímka přímé úměry)
Obr. 1: Závislost závisle proměnné od nezávisle proměnné, pokud je R = 1 (přímka přímé úměry)
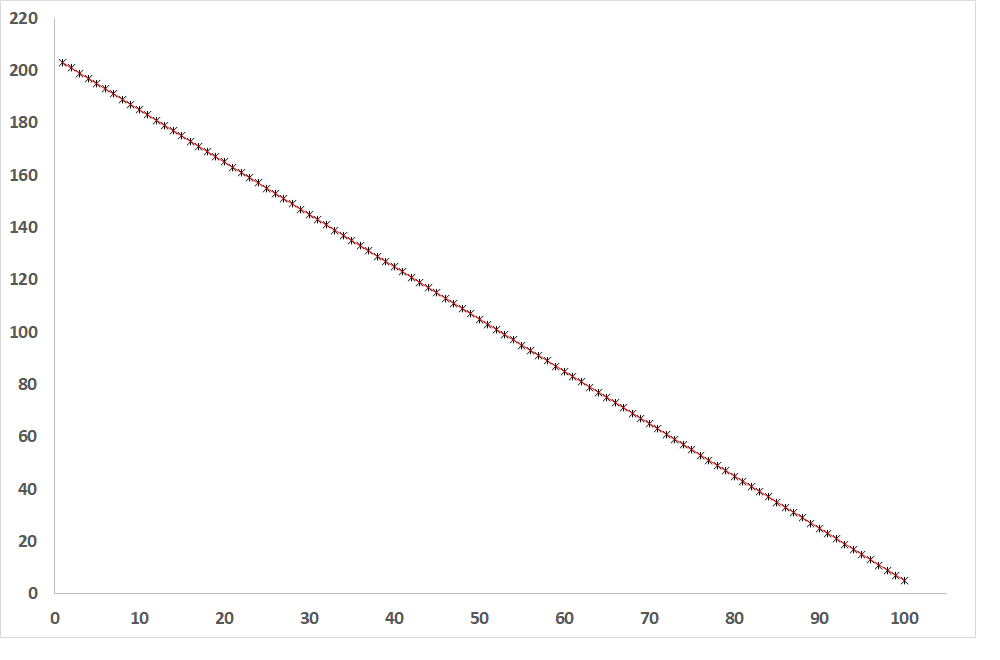 Obr. 2: Závislost závisle proměnné od nezávisle proměnné, pokud je R = -1 (přímka nepřímé úměry)
Obr. 2: Závislost závisle proměnné od nezávisle proměnné, pokud je R = -1 (přímka nepřímé úměry)
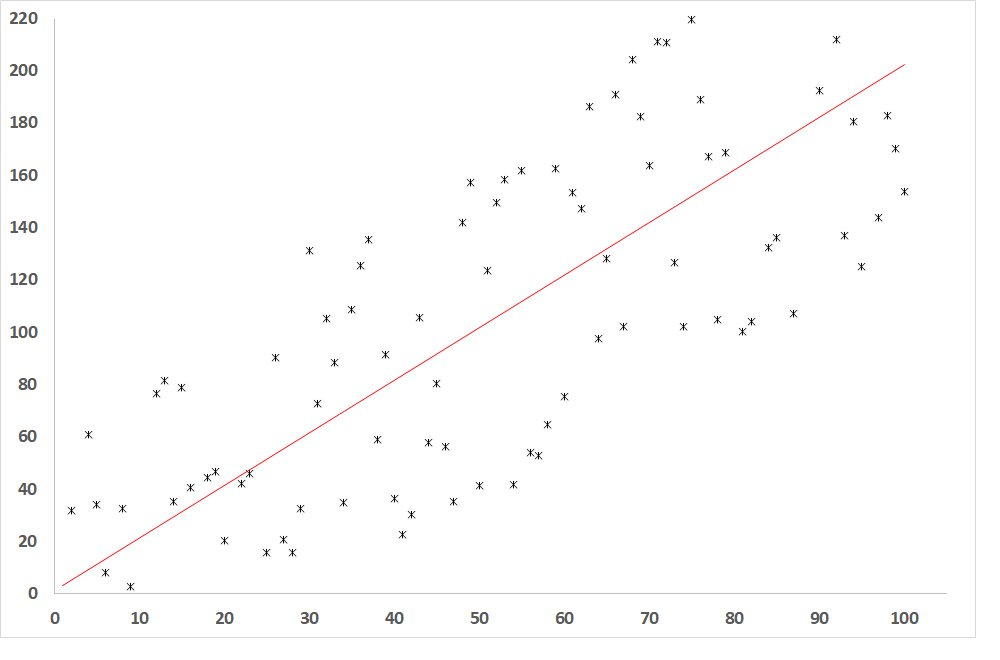
Obr. 3: Závislost závisle proměnné od nezávisle proměnné, pokud je R = 0,8 (relativně těsný vztah mezi proměnnými)
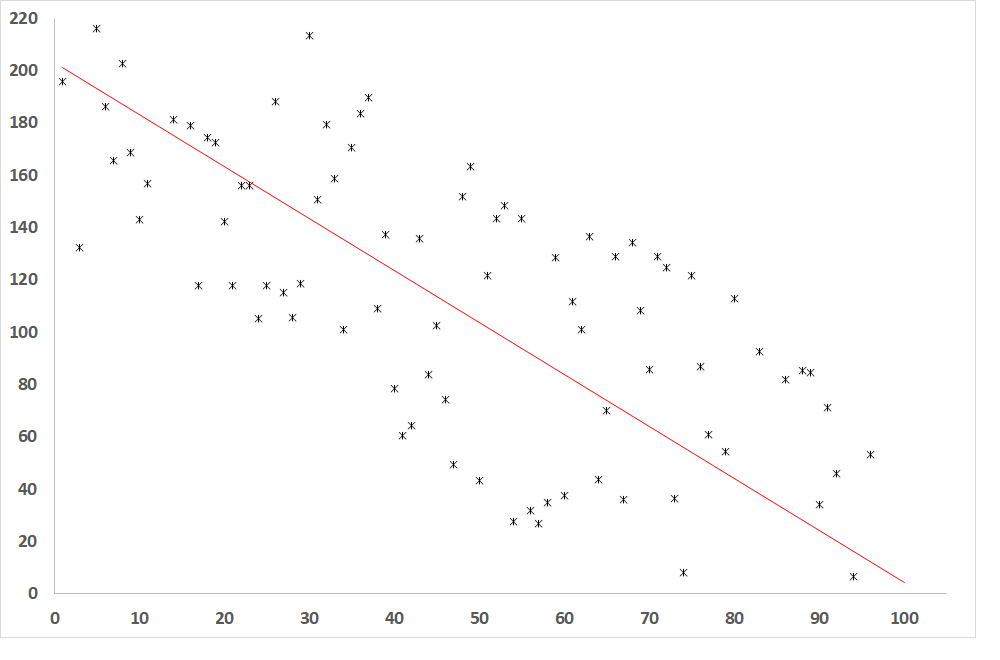
Obr. 4: Závislost závisle proměnné od nezávisle proměnné, pokud je R = -0,8 (relativně těsný vztah mezi proměnnými)
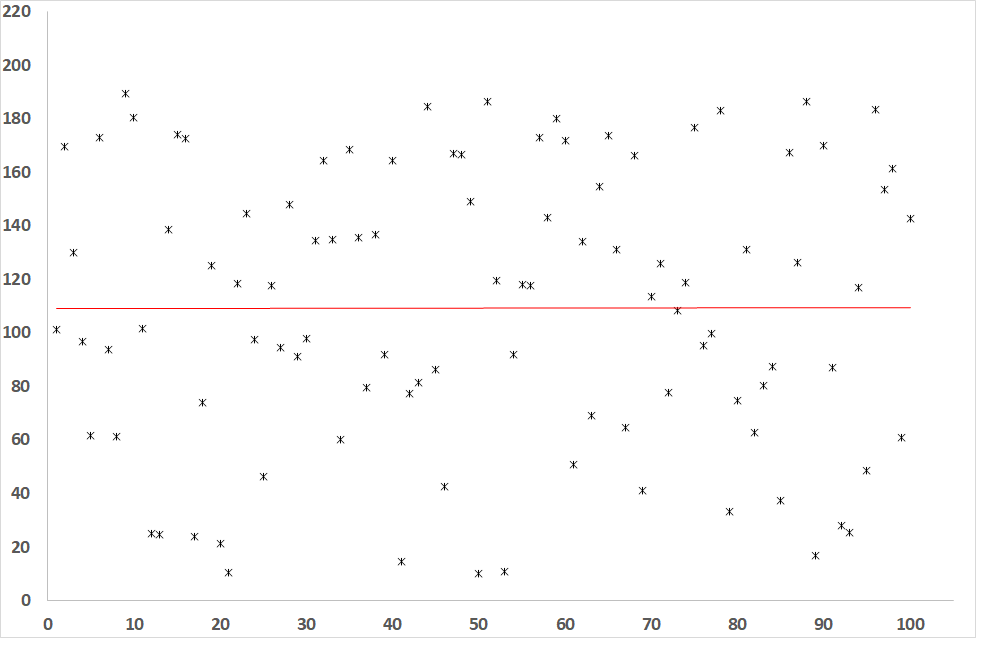
Obr. 5: Závislost závisle proměnné od nezávisle proměnné, pokud je R = 0 (není korelace mezi proměnnými)
Problematika korelace je rozsáhlejší, tento článek je stručným souhrnem. Pro hlubší studium doporučujeme navštívit některé ze školení, které poskytuje naše společnost.
Doporučená školení:
| Název školení | Délka školení | Volné termíny | Cena | |
|---|---|---|---|---|
| Základy SPC - Statistické metody řízení procesů |
1 den
|
09.02.2026
+ 9 dostupných termínů
|
5 500,00 CZK
6 655,00 CZK s DPH
|
Více o školení |
| SPC v automotive - podle příručky AIAG |
2 dny
|
10.02.2026
+ 5 dostupných termínů
|
9 500,00 CZK
11 495,00 CZK s DPH
|
Více o školení |
| SPC II - Řešení problémů SPC |
2 dny
|
Podle Vás
|
Na vyžádání | Více o školení |
| Six Sigma trénink |
2 dny
|
Podle Vás
|
Na vyžádání | Více o školení |
| SPC III - Projekt zavádění statistických metod v organizaci |
2 dny
|
Podle Vás
|
Na vyžádání | Více o školení |
| Inovativní metody využívané v automobilovém průmyslu a strojírenské výrobě |
11 dní
|
Podle Vás
|
Na vyžádání | Více o školení |